同源密码学
同源密码属于能抵抗量子攻击的后量子密码体制,基于椭圆曲线密码。
参考论文:1321.pdf (iacr.org),550.pdf (iacr.org)
前置知识
扩域
如果域$F$是$K$的子域,那么$K$是$F$的扩域或者域的扩张,记作$K|F$。例如对于某个有限域$F_p$,它的二次扩张为$F_{p^2}$。
超奇异同源Diffie-Hellman (SIDH) 秘钥交换算法就是在这个$F_{p^2}$有限域下工作的,可以知道这个有限域的大小为$p^2$,即为有$p^2$个元素,表示这个有限域元素的一个简便的表示方法就是写为复数形式:
$$
u+vi\ \ (u,v\in F_p)
$$
同源性
同源(isogeny)指的是两条椭圆曲线之间的同态。相当于把一条椭圆曲线的点映射到另一条椭圆曲线上。例如:对于在$F_q$的椭圆曲线$E_1,E_2$,对于映射$\phi:\phi(P_1)=P_2,P_1\in E_1,P_2\in E_2$可以称作一个同源。
同源映射到的曲线$E’$是这个同源的陪域(codomain)。
一些性质:
同源满足满同态,每一个映射后的曲线中的点都有原像与之对应。
同源将单位元映射成另一个曲线中的的单位元,将无穷远点也映射成另一个无穷远点。
自同态:椭圆曲线到自身的同源。
自同构:同源是自同态,也是同构。
自同态不一定是同源:
$$
\forall P\in E(K),\phi(P)=O
$$
不是满同态,不是同源。同构本身属于满同态,所以自同构一定是同源。
几个同源的例子:
①将点映射成它的逆元:
$$
\phi:E(K)→E’(K)
$$
$$
P=(x,y)\mapsto -P=(x,-y)
$$
是同源,是自同态,也是个自同构。
②把点映射成运算$n$遍后的点:
$$
\phi:E(K)→E’(K)
$$
$$
P\mapsto nP
$$
注意当$n=0$时,不满足同源,因为此时将所有的点都映射成无穷远点,不满足满同态。
只有当$n≠0$时才是同源;当$n=±1$时,是自同构。
Sato-Tate定理:$|E(F_q)|=|E’(F_q)|$当且仅当这两个曲线同源。
同源的标准形式
设$\phi:E(K)→ E’(K)$是同源($K$是域),点$P=(x,y)\in E(K)$,在仿射坐标下,$\phi$具有以下标准形式:
$$
\phi(x,y)=(\frac {u(x)}{v(x)},\frac{s(x)}{t(x)}y)
$$
其中$u(x),v(x),s(x),t(x)\in K[x]$,$u(x),v(x)$互素,$s(x),t(x)$互素。
从标准形式中可以看出,映射后的横坐标只和原像的横坐标相关,纵坐标和原像的横纵坐标都有关系。
把上面几个同源的例子拿过来说说:
①将点映射成它的逆元:
$$
\phi:E(K)→E’(K)
$$
$$
P=(x,y)\mapsto -P=(x,-y)
$$
在这种情况里:$u(x)=x,v(x)=e$,$s(x)=-e,t(x)=e$。
②把点映射成运算$n$遍后的点(我们取$2$测试):
$$
\phi:E(K)→E’(K)
$$
$$
P\mapsto 2P
$$
根据椭圆曲线的运算,可以得到:
$$
2P=(\frac{x^4-2ax^2-8bx+a^2}{4(x^3+ax+b)},\frac{x^6+5ax^4+20bx^3-5a^2x^2-4abx-a^3-8b^2}{8(x^3+ax+b)^2}y)
$$
对应着就可以写出四个参数。
推论:设$E(K)$方程为$y^2=x^3+ax+b$,$f(x)=x^3+ax+b$,有:
$$
v^3(x)|t^2(x)
$$
$$
t^2(x)|v^3(x)f(x)
$$
J-invariant值
同构曲线的J-invariant值用来判断两个椭圆曲线是否同构。如果两条曲线的J值相同说明他们同构。
比起我们常用的Weierstrass方程简化形式:
$$
E:{(x,y)|y^2=x^3+ax+b}
$$
介绍另一种蒙哥马利形式的椭圆曲线(Montgomery form),曲线方程表示为:
$$
E: y^2=x^3+ax^2+x
$$
计算其J-invariant值就是:
$$
J(E)=\frac{256(a^2-3)^3}{a^2-4}
$$
在论文1321中,取的有限域为$F_{431^2}$,存在蒙哥马利形式的两条曲线,两个参数$a$分别是:
$$
\begin{cases}a_1=208i+161\
a_2=172i+162\end{cases}
$$
可以简单验证两条曲线是否同构,通过计算J-invariant值:
1 | p = 2^4*3^3-1 |
这两条曲线同构,就是因为提供的两个参数$a$,通过计算$\frac{256(a^2-3)^3}{a^2-4}$发现结果相等。
在论文中使用了蒙哥马利曲线,因为对于蒙哥马利曲线之间的映射来说,可以简单使用$x$坐标来映射:
$$
(x,y) \rightarrow (f(x) , cyf’(x))
$$
当我们确定了$x$的映射函数之后,可以得到唯一确定的$y$的坐标,也不会存在多解,这里的$c$是一个不变的常数,$f’(x)$根据$f$函数单独确定。
我们知道椭圆曲线的无穷远点为单位元,如果我们能知道能映射到单位元的点,就可以将这些点构成集合,也就是这个映射的核,映射的核是正规子群,可以用来构造商群,可以进一步使用第一同构定理找到和映射的像之间的同构。
论文中提到一个将$E$映射到二倍点的例子,可以简化为:
$$
E \rightarrow E,\quad x \rightarrow \frac{(x^2-1)^2}{4x(x^2+ax+1)}
$$
根据这个映射可以知道这个映射的核,当分母为$0$时,即可得到无穷远点,求解方程即可得到核点的横坐标:
$$
4x(x^2+ax+1) = 0
$$
可以得到方程对应的三个解:$0,\alpha,\frac 1\alpha$,满足:
$$
\alpha^2+a\alpha+1 = 0
$$
代入曲线方程得到三个核中的点:
$$
(0,0),(\alpha,0),(\frac 1\alpha,0)
$$
根据同态性质,单位元映射到对应的单位元,所以核中包含四个点:
$$
K = {O,(0,0),(\alpha,0),(\frac{1}{\alpha},0)}
$$
此时,我们可以重新定义同源:
对于一条曲线$E$和$E$上的一个子群$G$,可构造一个以$G$为核的映射$\phi:E\rightarrow E’$,这个映射就是同源。
sage实现二倍点同源:
1 | #example |
在二倍点同源中,它的子群$G$不是一个循环群,因为群里除了单位元之外的阶都是$2$,没有生成元。
如果我们生成一个阶为$2$的循环子群作为子群$G={O,(\alpha,0)}$,可以使用这个子群和曲线$E$生成一个同源:
这里使用了$\alpha=350i+68$产生循环子群:
1 | p = 2^4*3^3-1 |
同源的度
同源的度是同源的核的大小,即为同源映射后$f(x)$分子分母多项式的度最大值,对于度为$d$的同源,记为$d-isogeny$。
对于上面的二倍点同源,核大小为$4$,同源度为$4$,是个$4-isogeny$;后面那个二阶循环群的同源的度就是$2$。
torsion
这里还存在一个新的概念torsion,对于一个椭圆曲线,满足:
$$
lP=O
$$
的$P$点构成的集合,就是$l-torsion$。
上面的二倍点映射的核是一个$E$上的$2-torsion$。
同源图
在之前第二个同源的例子中,我们取了$2-torsion$中的一个点,生成的循环子群$G$构造的同源使得$j-invariant$值发生了变化:
$$
364i+304\Rightarrow 344i+190
$$
此外,如果我们使用剩下除了单位元的两个点,也能构造出$j-invariant$值改变的同源:
$$
364i+304\Rightarrow 67
$$
$$
364i+304\Rightarrow 319
$$
对于一个二次扩域,所有的$p^2$个元素也就是$p^2$个$j$不变量,论文提到存在一个大小为$[\frac p{12}]+z,z\in\{0,1,2\}$的子集($z$和$p$的取值相关),这个子集恰好包含了所有二次扩域下的所有的$j$不变量。
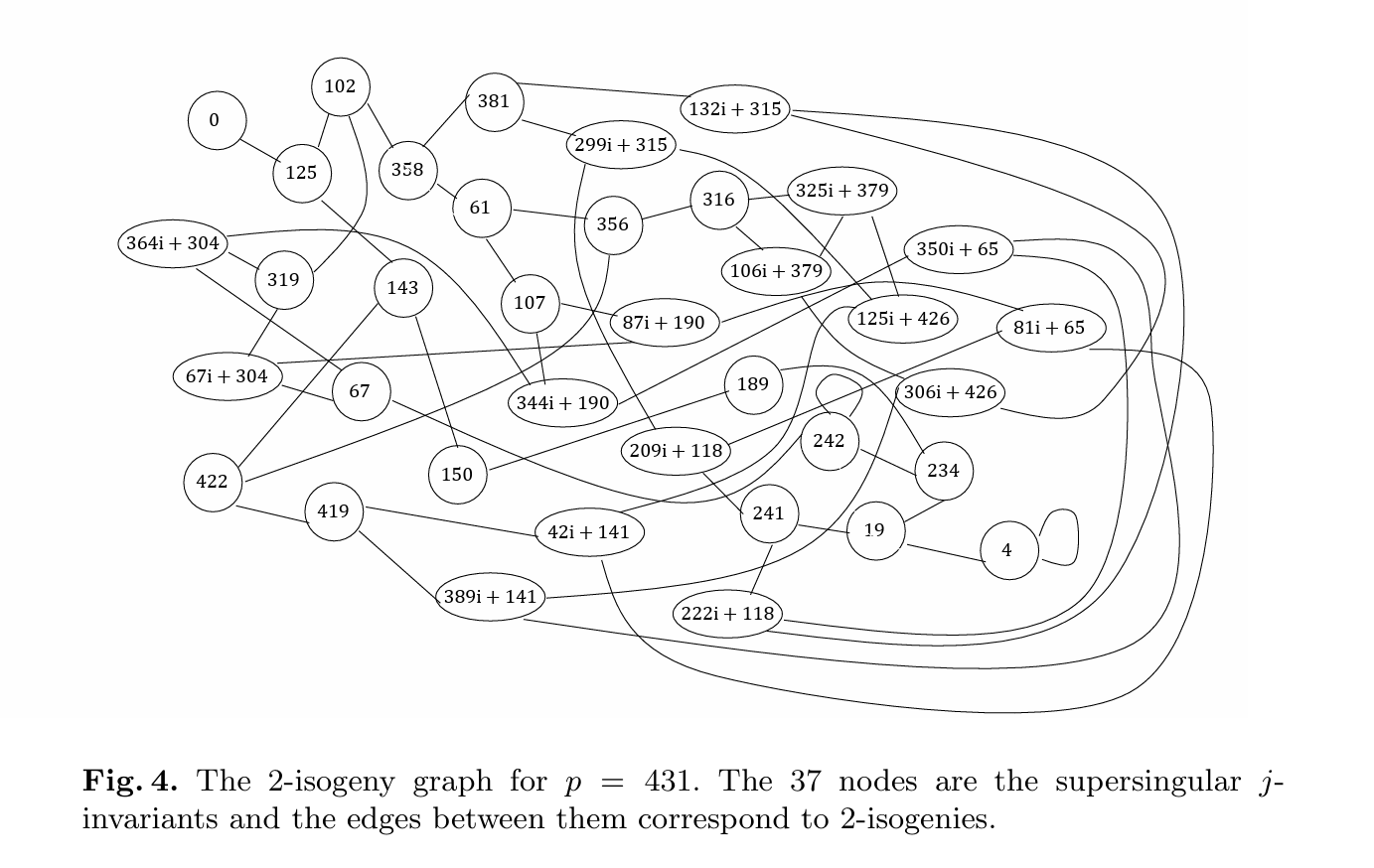
对于二次扩域$F_{431^2}$,存在大小为$37$的子集,子集中的每一个元素都代表着同构下的一条超奇异椭圆曲线的$j$不变量:
刚提到使用了不同的点构造出$j$不变量改变的同源映射,将对应的点用线连接,将所有的能构成映射关系的两个$j$不变量全部连接起来,能构成一个完整的$2-isogeny$同源图。
这里,我们根据$2-torsion$构造出所有的$2-isogeny$:
这里的边为无相边,揭示了映射是相互存在的,某个$E$对$E’$存在一个度为$2$的同源,那么$E’$也对$E$存在度为$2$的对偶同源。
图中还是有一些值得注意的地方:
对于点$0,4,242$等,邻居数较少,甚至出现了闭环。对于大部分的点,都是存在$3$个邻居的。
$2-isogeny$图提示出了度为$2$的同源的$j$不变量的移动,对于$3-isogeny$图也能用相同的方式构造出来。
两个度为$2$的同源,复合起来可以看做是度为$4$的同源。也就是:
度为$d^e$的同源可以拆解为$e$个$d$度的同源,在$d-isogeny$图上呈现一条$e$长度的路径。
modular polynomial
再提出一个新的定义,如果我们知道一个$j$不变量,可以代入modular polynomial求出根,得到的根就是作为邻居的$j$不变量,简单来说,这个模多项式用一个多项式关联了$d-isogeny$中互为邻居的$j$不变量。
一个度较低的多项式在线网站:Modular polynomials (mit.edu)
超奇异同源密钥交换算法
这里学习一下超奇异同源Diffie-Hellman (SIDH) 秘钥交换算法,SIDH据了解在2022年已经被攻破了。
这里的超奇异椭圆曲线是指$E$的阶在模数下为$1$的曲线,可以使用sage的E.is_supersingular()来验证。
参数选择
首先选择超奇异椭圆曲线$E$作为公开参数,Alice选择两个点$P_A,Q_A\in E$并公开,Bob也选择两个元素$P_B,Q_B\in E$并公开。
Alice选择秘密$s_A,t_A$作为秘密信息,计算$R_A=s_AP_A+t_AQ_A\in E$,通过点$R_A$建立一个有关群$E$的子群$E_A=\left \langle R_A \right \rangle$,计算得到一个从$E$映射到子群$E_A$的同源$\phi_A:E\mapsto E_A$。
同样,Bob选择秘密$s_B,t_B$作为秘密信息,计算$R_B=s_BP_B+t_BQ_B\in E$,通过点$R_B$建立一个有关群$E$的子群$E_B=\left \langle R_B \right \rangle$,计算得到一个从$E$映射到子群$E_B$的同源$\phi_B:E\mapsto E_B$。
秘密计算
Alice获得Bob的公开信息,计算$\phi_A(P_B),\phi_A(Q_B)$并公开,发送给Bob公开信息$E_A,\phi_A(P_B),\phi_A(Q_B)$。
Bob获得Alice的公开信息,计算$\phi_B(P_A),\phi_B(Q_A)$并公开,发送给Alice公开信息$E_B,\phi_B(P_A),\phi_B(Q_A)$。
Alice计算子群$E_{BA}$:
Alice需要计算得到$\phi_B(R_A)$,根据群同态的特点可以得到:
$$
\phi_B(R_A)=\phi_B(s_AP_A+t_AQ_A)=s_A\phi_B(P_A)+t_A\phi_B(Q_A)
$$
根据$\phi_B(R_A)$来得到子群$E_{BA}$。这个子群是以$\phi_B(R_A)$为同态核的群同态映射到$E$上的子群,这个同源也就是$\phi_{BA}$。
Bob也可以同样计算出子群$E_{AB}$,$E_{BA}$和$E_{AB}$是同构的(具体原因就不探究了),并且已有文献发现这两条曲线是相同的。所以共同秘密就可以定为他们的J-invariant值$J(E_{BA})=J(E_{AB})$。
代码实现
sage里内置了一些求解我们实现SIDH的相关函数:
1 | from Crypto.Util.number import * |
一些题目
Neighbors
1 | from Crypto.Util.number import * |
题目首先定义了一个在$p=2^{151}5^{172}-1$的$F_{p^2}$下的$J=1728$的超奇异椭圆曲线,以这个曲线为起点计算了一个度为$5^{50}$的同源到达曲线$E’$,使用$E’$的$j$不变量生成RSA的素数$p$,之后进行常规的RSA加密。
题目还进行了一个泄露信息过程,以$E’$为起点计算了一个度为$5^4$的同源,到达$E’’$,给出$E’’$的不变量$J_1$。
思路就是利用这个泄露利用模多项式关系得到$5^4-isogeny$距离的所有邻居,通过这些邻居尝试生成$p$,检查是否能被$n$整除,得到$n$分解,进行RSA加密。
1 | from Crypto.Util.number import * |