概念

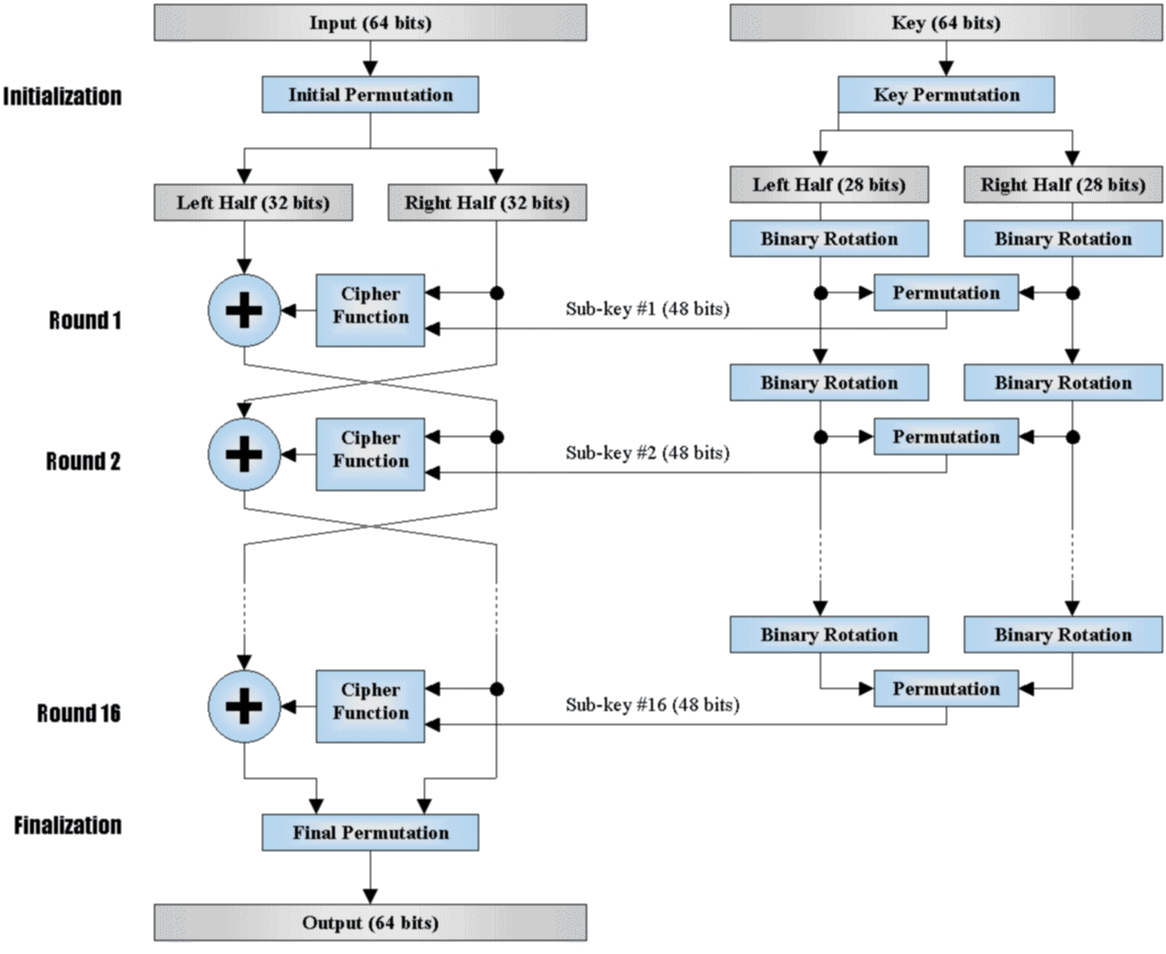
DES算法属于对称加密算法的分组加密算法。DES 使用一个 56 位的密钥以及附加的 8 位奇偶校验位，总共为64位，产生64位的分组，输入和输出块均为64位（八个bytes）。这是一个迭代的分组密码，加密结构也被称为是Feistel网络，其中将加密的文本块分成两半。使用子密钥对其中一半应用循环功能，然后将输出与另一半进行“异或”运算；接着交换这两半，这一过程会继续下去，但最后一个循环不交换。DES 使用 16 个循环，使用异或，置换，代换，移位操作四种基本运算。

密钥的每个第八位设置为奇偶校验位，密钥实际长度为56位。

加密流程

理解一下每一轮的加密流程：
$$
L_{i+1}=R_i
$$

$$
R_{i+1}=L_i\oplus F(R_i,K_i)
$$

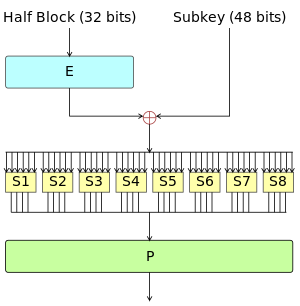
DES加密算法有四个步骤：初始置换、生成子密钥、迭代过程、逆置换。核心的部件包括初始置换和$F$函数（$E$扩展置换，$S$盒替代，$P$盒置换）以及逆置换，$F$函数的流程如图：

img

使用python进行DES加密时可以使用pyDes库进行加解密，也可以使用pycryptodome库的DES模块进行加解密，由于加密模式和AES加密中的模式都是通用的，所以就不举例子了。

初始置换

初始置换将原始明文经过IP置换表处理：

IP置换表中的数据指的是位置，例如58指将明文$M$的第一位放到58位上，根据IP表全部置换后成为$M’$。

M=0110001101101111011011010111000001110101011101000110010101110010
L0=11111111101110000111011001010111
R0=00000000111111110000011010000011

置换后，取$M’$的前32位为$L_0$，后32位为$R_0$。

生成子密钥

DES 加密共执行16次迭代，每次迭代过程的数据长度为48位，因此需要16个48位的子密钥来进行加密，生成子密钥的过程如下：

第一轮置换

K=0001001100110100010101110111100110011011101111001101111111110001

原始的64位密钥经过PC-1表采用和IP表同样的置换方式进行置换，PC-1表为8行7列的表，原始密钥$K$经过PC-1表后变为56位数据$K’$。

K‘=11110000110011001010101011110101010101100110011110001111

C0=1111000011001100101010101111

D0=0101010101100110011110001111

取$K’$前28位作为$C_0$，后28位作为$D_0$。

获得$C_0,D_0$之后进行循环左移操作，查询移动位数表：

1
2
轮数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
位数 1 1 2 2 2 2 2 2 1  2  2  2  2  2  2  1

进行第一轮移位，查表得知轮数1的位移量为1，$C_0,D_0$分别左移1位：

C1=1110000110011001010101011111

D1=1010101011001100111100011110

将$C_1,D_1$合并之后，再经过PC-2表置换，注意PC-2表没有了9,18,22,25,35,38,43,54位，得到一个$6×8$的表。最后的48位密钥就是$K_1$。

第二轮置换

$C_1,D_1$左移，差表得知位移量为2，左移2位得到$C_2,D_2$：

C2=1100001100110010101010111111
D2=0101010110011001111000111101

合并后经过PC-2表置换，得到48位密钥$K_2$。

后续子密钥以此类推。

迭代过程

把扩展置换$E$，S-盒替代，P-盒置换总过程称为函数$F$。

扩展置换

由于右半部分32位，密钥为44位，为了确保长度相等能进行异或，存在一个扩展置换表$E$，对右半进行扩展，经过扩展后变为48位数据。

扩展后进行异或运算。

S-盒替代

代替运算用八个S盒，每个S盒有六位输入，四位输出：

那么是怎么做到六位输入四位输出的呢？

例：S-盒1：

1
2
3
4
14,04,13,01,02,15,11,08,03,10,06,12,05,09,00,07,
00,15,07,04,14,02,13,01,10,06,12,11,09,05,03,08,
04,01,14,08,13,06,02,11,15,12,09,07,03,10,05,00,
15,12,08,02,04,09,01,07,05,11,03,14,10,00,06,13,

如果输入为110111：

第一位和最后一位组合为11，十进制为3，对应第三行。

中间四位1011对应十进制为11，对应11列，查表，得到值14，转为二进制1110，输出。

P-盒置换

将S-盒替代后的输出结果作为P-盒置换的输入，P-盒置换表如下：

1
2
16,07,20,21,29,12,28,17,01,15,23,26,05,18,31,10,
02,08,24,14,32,27,03,09,19,13,30,06,22,11,04,25,

逆置换

最终得到的L16和R16进行逆置换得到最终输出。

双重和三重DES

双重DES使用两个密钥，长度为112位：
$$
C=E_{k_2}(E_{k_1}(P))
$$

双重DES不能抵抗中间相遇攻击。

三重DES使用三个密钥：
$$
C=E_{k_3}(D_{k_2}(E_{k_1}(P)))
$$

$$
P=D_{k_1}(E_{k_2}(D_{k_3}(C)))
$$

在三重DES里，选择密钥有两种方式：

1.选择三个不同的密钥$k_1,k_2,k_3$，一共168位。

2.选择两个不同的密钥使得$k_1=k_3\not =k_2$，共112位。

攻击方式及赛题

DES已知一轮密钥

题目取自[NCTF2019]Reverse：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import os
import pyDes


flag = "NCTF{******************************************}"
key = os.urandom(8)

d = pyDes.des(key)
cipher = d.encrypt(flag.encode())

with open('cipher', 'wb') as f:
    f.write(cipher)

# Leak: d.Kn[10] == [0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1]

加密是给出了第十一轮的密钥，可以根据加密算法逆推还原密钥：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
import copy
import pyDes

key='********'
d=pyDes.des(key)
PC1=[56, 48, 40, 32, 24, 16, 8, 0, 57, 49, 41, 33, 25, 17, 9, 1, 58, 50, 42, 34, 26, 18, 10, 2, 59, 51, 43, 35, 62, 54, 46, 38, 30, 22, 14, 6, 61, 53, 45, 37, 29, 21, 13, 5, 60, 52, 44, 36, 28, 20, 12, 4, 27, 19, 11, 3]
PC2=[13, 16, 10, 23, 0, 4, 2, 27, 14, 5, 20, 9, 22, 18, 11, 3, 25, 7, 15, 6, 26, 19, 12, 1, 40, 51, 30, 36, 46, 54, 29, 39, 50, 44, 32, 47, 43, 48, 38, 55, 33, 52, 45, 41, 49, 35, 28, 31]
movnum = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]#对应16轮中每一轮的循环左移位数

def gen_key(C1,D1,k):
    tempc=C1
    tempd=D1
    for i in range(k):
        tempc = tempc[1:] + tempc[:1]
        tempd = tempd[1:] + tempd[:1]
    tempCD1=tempc+tempd
    tempkey=[]
    for i in range(len(PC2)):
        tempkey.append(tempCD1[PC2[i]])
    return (tempkey,tempCD1)#轮运算得到下一轮子密钥

def re_gen_key(C1,D1):
    tempc=C1[-1:]+C1[:-1]
    tempd=D1[-1:]+D1[:-1]
    tempCD1=tempc+tempd
    return tempCD1 #轮运算得到上一轮CD

def get_key(CD):
    tempkey=[]
    for i in range(len(PC2)):
        tempkey.append(CD[PC2[i]])
    return tempkey

def RE_pc2():
    CD1=['*']*56
    for i in range(len(PC2)):
        CD1[PC2[i]]=keyknow[i]#初步还原CD1
    results=[]
    for i in range(256):
        temp=bin(i)[2:].zfill(8)
        tempi=copy.deepcopy(CD1)
        d=0
        for j in range(len(tempi)):
            if tempi[j]=='*':
                tempi[j]=eval(temp[d])
                d=d+1
        results.append(tempi)
    return results


def decrypt(flag_enc,known):
    results=RE_pc2()
    for i in range(len(results)):
        temp=results[i]
        for j in range(sum(movnum[:known])):
            temp=re_gen_key(temp[:28],temp[28:])
        tempK=[]
        Z=temp
        for j in range(16):
            tempx=gen_key(Z[:28],Z[28:],movnum[j])
            tempK.append(tempx[0])
            Z=tempx[1]
        d.Kn=tempK
        print(d.decrypt(flag_enc))
 
if __name__ == "__main__":
    flag_enc=open('cipher','rb').read()
    keyknow=[0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1]
    known=11
    decrypt(flag_enc,known)

DES弱密钥攻击

DES的弱密钥如下：

1
2
3
4
5
6
7
8
0x0101010101010101
0xFEFEFEFEFEFEFEFE
0xE0E0E0E0F1F1F1F1
0x1F1F1F1F0E0E0E0E
0x0000000000000000
0xFFFFFFFFFFFFFFFF
0xE1E1E1E1F0F0F0F0
0x1E1E1E1E0F0F0F0F

所谓弱密钥，就是使用这种密钥，进行加解密时没有区别，所以就有：
$$
E_k(E_k(m))=m
$$
所以使用弱密钥作为密钥进行DES加密是极其不安全的，攻击者通过已知的弱密钥直接进行加密或者解密都可以直接得到明文。