LFSR

LFSR（线性反馈移位寄存器）属于FSR反馈移位寄存器的一种，另一种为NFSR（非线性反馈移位寄存器）。

LFSR使用明文二进制位作为密钥流发生器的种子，生成密文。

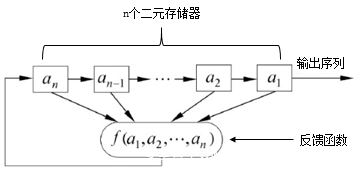
反馈寄存器（FSR）是流密码产生密钥流的一个重要组成部分，在模$2$有限域上的一个$n$级的FSR通常由$n$个二元存储器和一个反馈函数组成。

当反馈函数为线性时，就称为LFSR（线性反馈移位寄存器），反馈函数可以表示为：

$$f(a_1,a_2,...)=c_na_1\oplus c_{n-1}a_2\oplus...\oplus c_1a_n$$

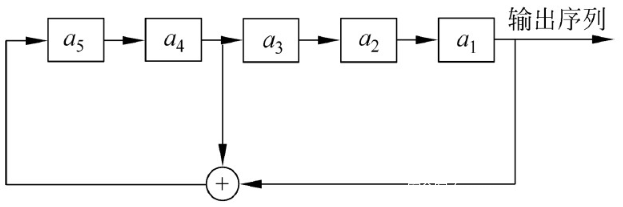
例如，假设一个五级的LFSR，初始状态为$(a_1,a_2,a_3,a_4,a_5)=(1,0,0,1,1)$，反馈函数为$f(a_1,a_2,a_3,a_4,a_5)=a_4\oplus a_1$，过程表示为：

然后会将反馈函数计算值作为$a_6$放在末尾，并且将$a_1$输出。

注意到$a_6=a_4\oplus a_1=0$，即为$a_n=a_{n-2}\oplus a_{n-5}$，所以可以通过表达式推出剩下的数值，通过计算发现从32位开始的数据开始呈现周期性变化。

即为五级LFSR的最大周期为$2^5-1$，可知对于$n$级LSFR的最大周期为$2^n-1$。周期达到最大的序列称之为$m$序列。

对于$n$级的LFSR，满足：

$$a_{n+k}=c_1a_{n+k-1}\oplus c_2a_{n+k-2}\oplus...\oplus c_na_k$$

这种递推关系可以用一个一元高次多项式表示：

$$p(x)=1+c_1x+...+c_{n-1}x^{n-1}+c_nx^n$$

这个多项式是LFSR的特征多项式。

$m$序列的伪随机

由于LSFR存在周期，生成的序列并不是毫无规律无穷无尽的，而是伪随机的。

游程：对于一串序列00110111，前两位为0的2游程，接下来是1的2游程，然后是0的1游程和1的3游程。

自相关函数：对于周期$T$的序列的自相关函数为：

$$R(\tau)=\frac 1T\sum^T_{k=1}(-1)^{a_k}(-1)^{a_{k+\tau}},0\leq\tau\leq T-1$$

可见，当$\tau=0$时，$R(\tau)=1$，当$\tau\not=1$，$R(\tau)$为异相自相关函数。

三个有关伪随机序列的随机性公设：

1.在一个周期内，0和1的个数相差最多为$1$。

2.在序列某个周期内，长为$1$的游程占游程数的$\frac 12$，长为$2$的游程占游程总数的$\frac 1{2^2}$，长为$i$的游程占游程总数的$\frac 1{2^i}$，且$0$的游程数和$1$的游程数相等。

3.异相自相关函数为一个常数。

$m$序列满足如上的三个随机性公设。

对于$m$序列，游程总数为$2^{n-1}$。

$m$序列的破译

已知$n$级反馈移位寄存器，如果能知道$2n$长度的连续序列，就可以利用矩阵进行破译。

例如，对于已知$5$级的LFSR，截获密钥流110100100001011，可以如下求解：

$$(a_6,a_7,a_8,a_9,a_{10})=(c_5,c_4,c_3,c_2,c_1)\begin{bmatrix}a_1&a_2&a_3&a_4&a_5\\a_2&a_3&a_4&a_5&a_6 \\a_3&a_4&a_5&a_6&a_7\\a_4&a_5&a_6&a_7&a_8\\a_5&a_6&a_7&a_8&a_9\end{bmatrix}$$

通过求解逆矩阵，运算即可得到$c$向量。

代码实现

对于位运算t & 0xffffffff，和1运算不会改变原始值，但是如果t位数过大会将t位数缩减到和0xffffffff相同位，作用是防止防止运算结果溢出到大于0xffffffff（这个上限可以改变）。

def lfsr(R,mask):
    output = (R << 1) & 0xffffffff
    i = (R & mask) & 0xffffffff
    lastbit = 0
    while i != 0:
        lastbit ^= (i & 1)
        i = i >> 1
    output ^= lastbit
    return (output,lastbit)

output = (R << 1) & 0xffffffff

这里将整个序列全部左移一位，去掉最高位并在最低位补0。

这里的mask为掩码，需要保密，需要与$R$相同二进制位数。

对于循环：

lastbit = 0
while i != 0:
       lastbit ^= (i & 1)
       i = i >> 1

这个循环实质上对$i$的每二进制位从后往前进行了异或。事先对lastbit设置为$0$，所以第一次运算结果就为i & 1。此外，可以发现在模$2$域下进行的异或运算和按位与运算的实质就是加法和乘法：

lastbit = lastbit + (i * 1)

output ^= lastbit

加密的最后对output再进行一次异或，先前得到output为R左移1位补一个0，现在相当于加上了lastbit的值。

实际加密时一般使用以下加密方式：

def lfsr(R,mask):
    output = (R << 1) & 0xffffffff
    i = (R & mask) & 0xffffffff
    lastbit = 0
    while i != 0:
        lastbit ^= (i & 1)
        i = i >> 1
    output ^= lastbit
    return (output,lastbit)

f=open("enc","w")
sum_enc = # 需要生成的密文总长
R = plaintext
mask = ...
for i in range(sum_enc):
    tmp=0
    for j in range(8): # 进行8次循环是因为，8次循环得到的8个二进制位恰好是一个字节的长度
        (R,out) = lfsr(R,mask)
        tmp = (tmp << 1) ^ out
    f.write(chr(tmp))

最终组合出的明文为LFSR加密中得到的所有lastbit组合形成八位字节密文。

为了更好的理解这种算法以及更好的运用在CTF的题目中，做几道简单的题。

[CICSN2018]oldstreamgame

flag = "flag{xxxxxxxxxxxxxxxx}"
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==14

def lfsr(R,mask):
    output = (R << 1) & 0xffffffff
    i=(R&mask)&0xffffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)

R=int(flag[5:-1],16)
mask = 0b10100100000010000000100010010100

f=open("key","w")
for i in range(100):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()

flag为八位16进制数字，先找找规律，mask里的3,5,8,12,20,27,30,32位为1，其他位都是0。

异或实质是二进制加，所以当i中有奇数个1的时候lastbit为1，有偶数个1的时候lastbit为0。而且i是根据R和mask操作得到的，所以当R中的第3,5,8,12,20,27,30,32位有奇数个1的时候lastbit为1，有偶数个1的时候lastbit为0。

也就是说，lastbit的值取决于R中的第3,5,8,12,20,27,30,32位异或结果。

$$lastbit=R_3\oplus R_5\oplus R_8\oplus R_{12}\oplus R_{20}\oplus R_{27}\oplus R_{30}\oplus R_{32}$$

这就是我们的反馈函数$f$的表达式。

提供的key文件转化为二进制数为798位，前补2位0刚好是800位，

当我们要输出第32位lastbit时，R已经左移了31位，此时的32位就是原来的第一位。

求第一位：?0010000011111101111011101111100

变成key：00100000111111011110111011111000

根据上面求lastbit的公式，得到：

$$?=R_3\oplus R_5\oplus R_8\oplus R_{12}\oplus R_{20}\oplus R_{27}\oplus R_{30}\oplus lastbit$$

也就是：

$$R_1=1\oplus 1\oplus 0\oplus 0\oplus 0\oplus 1\oplus 0\oplus 0=1$$

同样的方法，先右移，可以继续求得第二位等等。

from Crypto.Util.number import *

key = "00100000111111011110111011111000"
mask = "10100100000010000000100010010100"

R = ""
tmp = key

for i in range(32):
    newkey = "?" + key[:31]
    m = (
        int(newkey[-3])
        ^ int(newkey[-5])
        ^ int(newkey[-8])
        ^ int(newkey[-12])
        ^ int(newkey[-20])
        ^ int(newkey[-27])
        ^ int(newkey[-30])
        ^ int(tmp[-1 - i])
    )
    R += str(m)
    key = str(m) + key[:31]


flag = "flag{" + hex(int(R[::-1], 2)) + "}"
print(flag)

[强网杯2018]streamgame1

from flag import flag

assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag) == 25


def lfsr(R, mask):
    output = (R << 1) & 0xFFFFFF
    i = (R & mask) & 0xFFFFFF
    lastbit = 0
    while i != 0:
        lastbit ^= i & 1
        i = i >> 1
    output ^= lastbit
    return (output, lastbit)


R = int(flag[5:-1], 2)
mask = 0b1010011000100011100

f = open("key", "ab")
for i in range(12):
    tmp = 0
    for j in range(8):
        (R, out) = lfsr(R, mask)
        tmp = (tmp << 1) ^ out
    f.write(chr(tmp))
f.close()

# b'U8\xf7B\xc1\r\xb2\xc7\xed\xe0$:'

这道题目就用了LFSR进行加密，读完题目可以知道flag内容为19位二进制数，可以直接利用LFSR在已知的19位明文空间内进行遍历爆破，与所给加密字节比较，可以得到原flag。

这里的流密码生成存在循环，但是循环长度大到不可能跑完循环，所以不必担心会出现多重解的问题。

from Crypto.Util.number import *

def lfsr(R, mask):
    output = (R << 1) & 0xffffff
    i = (R & mask) & 0xffffff
    lastbit = 0
    while i != 0:
        lastbit ^= (i & 1)
        i = i >> 1
    output ^= lastbit
    return (output, lastbit)

with open('key', 'rb') as file:
    f = file.read()

mask = 0b1010011000100011100
for flag in range(2**19):
    R,a = flag,1
    for i in range(12):
        tmp = 0
        for j in range(8):
            (R, out) = lfsr(R, mask)
            tmp = (tmp << 1) ^ out
        if tmp != f[i]:
            a=0
            break
    if a:
        print('flag{'+str(bin(flag))[2:]+'}')
        break

在遍历时也要注意算法优化的问题，通常可以进行逐位检查，例如我们生成的第一位和题目生成的第一位如果不一样，后面的就不用再比较了，肯定不是我们要的那个19位数。通过以上优化，大约在10秒多就可以得到flag。

[强网杯2018]streamgame2

from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==27

def lfsr(R,mask):
    output = (R << 1) & 0xffffff
    i=(R&mask)&0xffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)

R=int(flag[5:-1],2)
mask=0x100002

f=open("key","ab")
for i in range(12):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()

#b'\xb2\xe9\x0e\x13\xa0j\x1b\xfc@\xe6}S'

跟上一题几乎是一模一样，除了扩大了一下明文空间，不过不影响爆破：

from Crypto.Util.number import *

def lfsr(R, mask):
    output = (R << 1) & 0xffffff
    i = (R & mask) & 0xffffff
    lastbit = 0
    while i != 0:
        lastbit ^= (i & 1)
        i = i >> 1
    output ^= lastbit
    return (output, lastbit)

with open('key', 'rb') as file:
    f = file.read()

mask = 0x100002
for flag in range(2**21):
    R,a = flag,1
    for i in range(12):
        tmp = 0
        for j in range(8):
            (R, out) = lfsr(R, mask)
            tmp = (tmp << 1) ^ out
        if tmp != f[i]:
            a=0
            break
    if a:
        print('flag{'+str(bin(flag))[2:]+'}')
        break